실험 주제
기-액 평형 실험 장치를 이용해 물과 에탄올의 단증류 실험을 수행한다.
실험 목적
단증류 실험을 진행함으로써 실험 장치의 사용법 및 물질 전달의 과정과 관련된 이론을 이해하고, 실험 과정에서 발생한 유체의 양과 조성에 따른 실험값과 이론값의 차이를 확인해 오차의 정도를 비교해 본다.
이론적 배경
1) 증류에 대해
증류란 끓는점의 차이를 이용해 액체 상태의 혼합물을 분리하는 방법이다. 석유화학공정에서 원유를 증류해 휘발유, 경유, 등유 등으로 분리하는 것이 대표적인 예시이고, 공기를 증류해 아르곤과 같은 특수한 기체를 얻는데 이르기까지 광범위하게 사용된다.
증류는 기-액 평형 관계를 기초로 한다. 2성분계를 함유한 액체 혼합물에서 발생하는 증기의 조성은 일반적으로 혼합물의 조성과 다르다. 증기와 액체의 관계를 나타낼 수 있는 것이 2성분계의 기-액 평형 관계이고, 기-액 평형이란 기체와 액체가 존재하는 경우, 계 내, 두 상의 조성, 온도, 압력이 일정하게 된 상태로 열역학적 임의 성분의 두 상의 화학포텐셜이 동등하게 된 상태를 말한다.
증류 조작은 대부분의 경우, 일정 압력하에서 일으키는 것이 보통이므로 일정 온도하에서의 기-액 평형 관계보다도 일정 압력하에 있어서의 기-액 평형 관계가 보다 중요하며 직접 유용한 것이 된다. 일정 온도하에서의 관계는 증류에서 보다 흡수 조작에서 필요하다.
그런데 증류란 일반적으로 2가지 이상 되는 휘발성 액체의 혼합물을 기화시켜서 각 성분을 되도록 순수한 상태로 분리하고자 하는 방법이고, 예로부터 실험실에서 공업적으로 널리 이용된 단위조작 중 하나이다. 증류에 의해 몇 개의 휘발성 성분을 분리할 수 있는 근본원리는 액체 혼합물의 조성과 그것으로부터 발생하는 증기의 조성이 다르다는 점이다.
2) 라울의 법칙(Raoult’s law)
어떤 특별한 경우에는 순수한 성분의 증기압 데이터로부터 어떤 농도범위에 있어서 용액의 비점 곡선을 나타낼 수가 있는 것이 라울의 법칙이다. 라울의 법칙은 일정한 온도에서 혼합물 중의 한 성분의 분압은 그 성분의 몰분율에다 같은 온도에서 그 성분이 순수한 상태에서 나타내는 증기압을 곱한 것과 같다는 것이다. 전 농도범위에서 완전히 들어맞는 경우란 극히 드물게 밖에 존재하지 않는다. 다시 말하면 한 성분의 분압은 그 성분의 몰분율이 0에서부터 1로 변화함에 따라서 0으로부터 완전한 증기압 사이에서 직선적으로 변화한다.
일정 온도에서 액체 혼합물 중 A성분의 분압 p_a, 그 성분의 순수한 상태에서의 증기압을P_a, 액체의 몰분율을 x_a로 하고, 같은 방법으로 이 혼합물의 B성분에 대해서도 표현하면 다음과 같다.
A성분의 분압 : p_a = P_a * x_a
B성분의 분압 : p_b = P_b * x_b
p_b = P_b * (1 – x_a), (x_a + x_b = 1)
위 식을 라울의 법칙(이상용액의 법칙)이라고 한다. 이 법칙이 전농동 범위에서 완전히 들어맞는 경우란 극히 드물지만, 몰분율 x = 0 ~ 1의 전 영역에 걸쳐서 성립하는 액체 혼합물을 이상용액 이라고 한다.
3) 단증류에 대해
단증류란 일정량의 혼합물을 증류기에 넣고, 열을 가해 끓인 후, 발생하는 증기를 응축기로 냉각시켜 유출액을 얻는 증류 방법이다. 주로 불순물이 고체인 경우 사용하고, 액체 불순물이 섞여 있을 때는 끓는점 차이가 비교적 큰 액체 혼합물에 적용한다. 끓는점 차이가 크지 않은 물질의 분리가 힘들어 분리 효율이 좋지 않다는 단점을 갖고 있지만 신속하고 저렴하다는 장점이 있어 널리 사용되는 방법이다.
단증류에서 혼합물 중의 휘발성 물질이 증발함에 따라 증류기에 남아 있는 용액의 양과 조성은 계속 변화한다. 이론적으로 이들의 관계는 다음과 같이 알 수 있다. 단증류를 시작한 후 어떤 순간에 증류기 내의 액량을 W, 상대적으로 낮은 끓는점을 갖는 성분의 질량분율을 x라고 하면 증류기 내에는 W_x의 저비점 성분이 있게 된다.
이때, 액과 평형상태에 있는 증기 중의 저비점 성분의 질량분율을 y라고 하면, dW만큼 증류되었다고 할 때, 유출액 중의 저비점 성분의 양은 dW_y가 되고, 증류기 내에 남은 액량은 (W – dW)이다. 이것의 질량분율은 (x - dx)가 되며, 증류기 내에 남은 저비점 성분의 양은 (W - dW) * (x - dx)가 된다. 따라서 총괄 물질 수지식은 다음과 같게 된다.
W_x = ydW + (W - dW) * (x - dx)
여기서 2차 미분항을 무시하고 정리하면 다음과 같다.
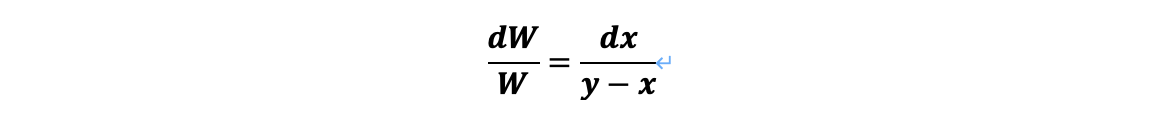
최초 증류기 내 액량 W₁로부터 단증류 후의 증류기 내 액량을 W₂라고 할 때, 이에 따른 액의 조성 변화인 x₁으로부터 x₂까지 적분하면 아래와 같은 “Rayleigh 식”을 얻을 수 있다.

원료에 대한 유출액 양의 비인 β는 아래 식 형태로 정의 가능하다.
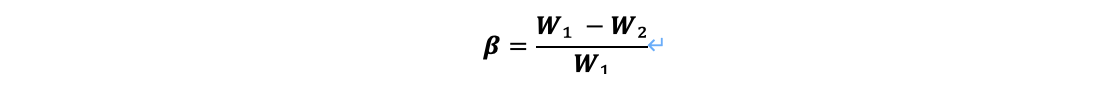
이를 위의 Rayleigh 식에 대입해 정리하면 아래 식을 얻는다.

앞서 소개된 수식의 우변(S)는 다음 형태로 표현될 수 있다. 여기서, 1/(y - x)를 0부터 x₁까지, 그리고 0부터 x₂까지 적분한 각 term을 I₁ 및 I₂로 정의하기로 한다.

유출량을 D, 유출액의 평균 조성을 x_Dav라고 하면, 물질 수지식은 아래와 같다.
W₁ - W₂ = D
W₁ * x₁ - W₂ * x₂ = D * x_Dav
이를 유출액 평균 조성에 대해 정리하면 다음과 같다.
x_Dav = (W₁ * x₁ - W₂ * x₂) / (W₁ - W₂)
즉, 단증류 전, 증류기 내 액량 W₁, 단증류 후의 증류기 내 액량 W₂, 그리고 증류 전, 후 조성 x₁, x₂을 통해서 유출액의 평균 조성 x_Dav 예측이 가능하다. 원료의 양과 조성 및 잔류액의 조성을 아는 경우, Rayleigh 식 및 그래프를 통해 W₂를 확인해 유출액의 이론적 평균 조성을 예측할 수 있다는 의미이다.
4) 단증류 외 증류법
단증류 외 증류법으론 평형증류, 수증기증류, 진공증류(감압증류) 등이 있다. 먼저 평형증류 (Equilibrium distillation)는 원료액에서 발생하는 증기와 잔류액이 항상 평형상태에 있는 조건하에서 증기와 잔류액을 분리하는 증류법이다. 이는 석유화학공업에서 원유의 경질유분을 대충 분리하는 조작으로, 석유 정류의 전처리 증류로 이용된다. 이는 플래시 증류, 적분 증류라고도 불리며, 다음과 같은 개략도를 갖는다.
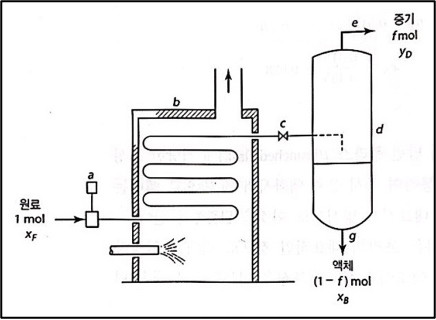
공급원료는 펌프 a로부터 가열기 b를 거쳐 c에 의해 압력이 감소된다. 접촉을 잘 이루는 증기와 액체 혼합물은 증기분리기인 d로 들어가면 오랜 시간에 걸친 뒤, 증기와 액체 부분으로 갈라진다. 증기는 e를 통해, 액체는 g로 나간다.
수증기 증류(Steam distillation)의 경우, 물과 혼합되지 않고 100℃ 근처에서 큰 증기압을 갖는 물질에 뜨거운 수증기를 뿜어 넣어 수증기와 함께 증류하는 방법이다. 혼합물이 가열되면 개개의 물질이 단독으로 가열되었을 때와 같은 증기압을 나타내므로 이들의 증기압과 수증기의 압력의 합이 대기압과 같아지면 증류되어 나와 각각의 끓는점 보다 훨씬 저온에서 증류할 수 있다. 따라서 보통의 증류법으론 분해될 우려가 있는 물질 또는 끓는점이 높은 물질의 분리정제에 이용된다.
이때, 수증기는 열원의 역할을 함과 동시에 증류 목적물의 분압을 낮추고 비점을 낮게 하는 역할을 한다. 기상 중의 수증기분압 p_s와 증류 목적성분의 분압 p_b의 한계는 전압 P와 같고, 기상 중의 수증기의 몰수와 목적성분의 몰수와의 비는 분압의 비와 같은 것을 알 수 있다. 따라서 위 내용을 수식으로 표현하면 다음과 같다. W는 중량, M는 분자량을 의미한다.

진공증류(Vacuum distillation)의 경우, 증류할 성분의 증기압이 작은 경우에 상압에서 증류하면 고온이 필요하므로 원료의 열분해 등 위험성이 있다. 이것을 방지하기 위해 감압으로 해서 비점을 저하시켜 고비점 성분의 증류, 정류를 하는 조작 방법이다. 이는 감압증류라고도 불린다.
액체의 비점은 액체의 증기압이 외부 압력과 같아지는 온도이므로 액체를 증류할 때 외부 압력이 대기압인 경우가 가장 간단하지만 정상 비점 이하에서 화합물이 분해 또는 산화되거나 분자의 재배열이 일어나는 등의 열에 민감한 물질들을 취급하는 데 있어서는 보통의 일반적인 증류 방식으로는 분리가 불가하다.
이렇듯 열에 매우 민감한 물질들을 증류하는 데 있어 주요한 조건은 낮은 증발 압력이다. 압력을 낮추면 증기압이 낮아지고 증발에 필요한 온도 또한 낮아진다. 따라서 비점을 더 낮출 필요가 있는 경우, 진공증류를 사용한다. 이때 사용되는 식은 클라우시우스-클라페이런 방정식이고, 수식은 다음과 같다.
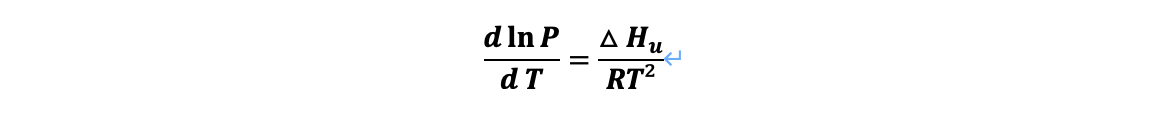
여기서 P는 포화증기압, T는 절대온도, R는 기체상수, △H_u는 증발잠열이다. 이 증발잠열의 온도에 의한 변화가 일정하다고 가정 후, 적분하면 다음과 같은 식이 표현된다.
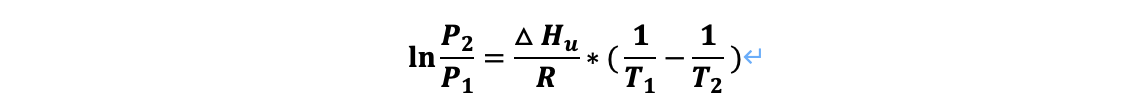
이상의 관계는 기-액간의 변화에 대해 적용할 수 있는 것인데, 고체-기체 간의 승화나 고체-액체 간의 용해 등의 현상에는 유사한 식이 성립한다.
실험 장치 및 방법
1) 실험 장치
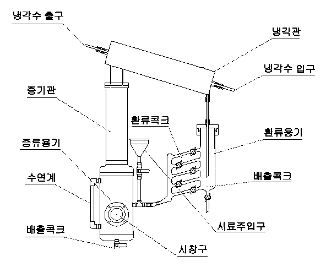
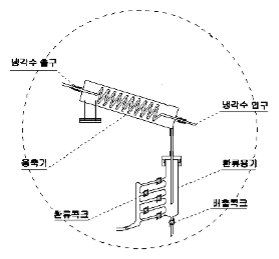
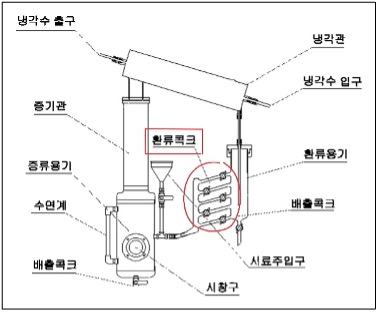
실험 장치 중 증류 용기에는 시료를 1.5리터 정도 넣을 수 있다. 증류의 열원은 용기 외벽을 감싸고 있는 히터로 되어 있고, 온도 조절은 실험 장치 좌측에 따로 배치된 전기 조작 패넬로 조절할 수 있다. 증기관을 통해 올라온 증기는 응축기가 응축을 시키며 증기를 냉각시킨다. 냉각된 응축수는 용기에 받아지고, 다시 이 응축액을 증류 용기로 환류관을 통해 보낸다. 환류관은 4개의 콕을 통해 혼합용액의 농도와 온도 변화를 측정하고, 환류관의 재질은 열충격 및 온도의 급격한 변화에 저항성을 가지는 Pyrex glass로 이뤄져 있다.
2) 실험 방법
a) 50ml 빈 비중병과 에탄올을 채운 비중병, 물을 채운 비중병, 혼합시료를 채운 비중병의 무게를 각각 측정한다
b) 혼합시료를 제조 후, 시료 주입구로 주입한다.
c) 용액이 단증류 장치 내에 있는지 확인 후, 메인 전원 버튼을 눌러 가동시킨다.
d) 배출콕크를 잠그고 나머지 밸브를 개방한다.
e) 수도를 열어 장치 내로 냉각수가 흐르도록 한다.
f) 장치 상의 히터 컨트롤을 6~7 사이로 맞춘다.
g) 용액이 응축되어 평형을 이룰때, 잔류부 및 유출부 각각에서 용액을 50mL 이상 추출
h) 비중병에 용액을 담아 무게를 측정한다.
3) 주의 사항
a) 비중병에 용액을 가득 채워 측정한다.
b) 용액 없이 증류장치 가열을 금지한다.
c) 응축 부의 온도 유지를 위해 냉각기 내 냉각수를 유입한다. *수도 밸브는 반드시 연다.
실험 결과 및 고찰
| 비중병 + 용액 [g] | 빈 비중병 [g] | 용액 [g] | |
| 1번(물) | 41.66 | 16.63 | 25.03 |
| 2번(에탄올) | 37.18 | 16.91 | 20.27 |
| 3번(물 + 에탄올) | 40.76 | 18.01 | 22.75 |
| 4번(유출액) | 38.35 | 17.11 | 21.24 |
| 5번(잔류액) | 41.06 | 18.03 | 23.03 |
표 1. 비중병을 이용한 각 성분의 무게
| 무게 [g] | |
| 빈비커 | 126.79 |
| 수용액 + 빈비커 | 406.34 |
| 유출액 + 빈비커 | 190.38 |
| 잔류액 + 빈비커 | 333.17 |
| 손실액 | 9.58 |
표 2. 비커를 이용한 각 성분의 무게
표1과 표2는 단증류 실험 데이터를 표로 나타낸 것이다. 증류 직후 계기판에 표시된 온도는 82℃였고, 실험 전 잔류부에 남아있던 수용액의 무게는 비커 합 406.34g이었다. 수용액의 조성은 물과 에탄올의 합이었고, 이 수용액을 증류해 얻은 유출액과 잔류액의 무게를 통해 손실액이 9.58g인 것을 알 수 있었다. 단증류 실험에서 각 성분과 시점에 따른 상태를 표1과 같이 1번에서부터 5번까지로 나타낼 때, 각 번호의 상대적 무게를 비교하면 다음과 같아야 한다.
1번(물) > 5번(잔류액) > 3번(수용액) > 4번(유출액) > 2번(에탄올)
표1과 같이 실제 실험 데이터 값이 위와 같은 형태를 띠므로 이번 실험이 정상적으로 진행되었음을 알 수 있다. 먼저 표1의 1번, 비중병을 이용한 물의 밀도 측정을 짚고 넘어가고자 한다. 1번의 경우, 비중병의 무게가 16.63g이고, 비중병 + 물의 무게가 41.66g으로 물의 무게는 25.03g이다. 25mL 기준의 비중병을 이용해 측정했으므로 이번 실험에 사용된 물의 밀도는 1과 같다고 볼 수 있다. 이와 같이 표1의 각 번호별 밀도를 구하면 다음 표 3과 같다.
| 용액 [g] | 밀도 [g/25mL] | |
| 1번(물) | 25.03 | 1.00 |
| 2번(에탄올) | 20.27 | 0.81 |
| 3번(물 + 에탄올) | 22.75 | 0.91 |
| 4번(유출액) | 21.24 | 0.85 |
| 5번(잔류액) | 23.03 | 0.92 |
표 3. 비중병을 이용한 각 성분의 밀도
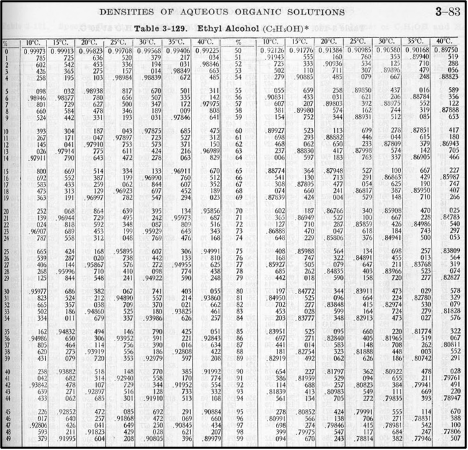
위 그림3, 밀도 표를 이용해 수용액과 잔류액 및 유출액 속 에탄올의 조성을 계산한다. 이때 비중병 측정 직전 잔류액의 온도는 29℃였고, 수용액과 유출액의 온도는 20℃로 가정한다. 따라서 내삽을 이용한 계산 시 결과는 다음과 같다.

위 계산에서 잔류액의 경우, 30℃에서 밀도가 0.92일때와 25℃에서 밀도가 0.92일 때 각각의 조성을 구한 뒤, 두 값의 내삽을 통해 최종적으로 밀도가 0.92, 온도가 29℃일 때의 에탄올 조성을 계산했다.
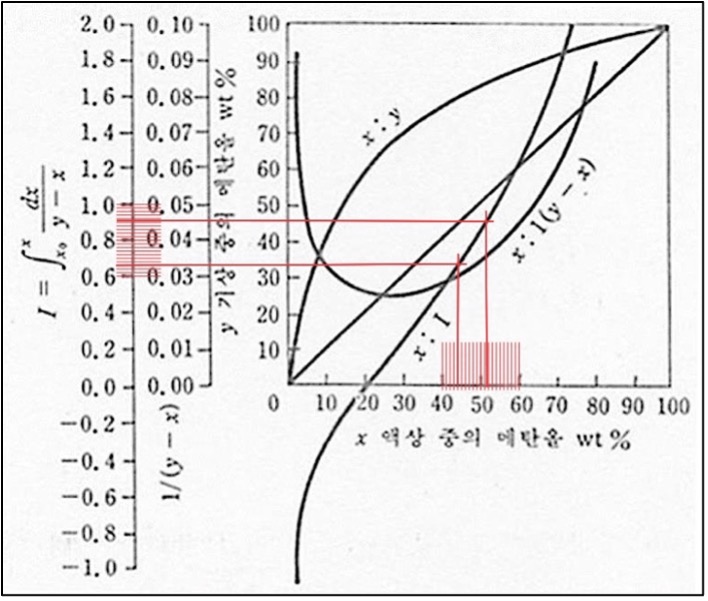
x_aqu와 x_res를 이용해 I값을 구하고자 한다. 이때 증류 전 잔류부의 수용액의 경우 I₁, 증류 후 잔류부의 잔류액을 I₂라고 표시한다. 그림4와 같이 최대한 정확도를 높이고자 일정한 간격의 선을 그래프에 추가하여 각 𝑥에 따른 I를 측정했다. 결과는 다음과 같다.
I₁ = 0.91, I₂ = 0.66
증류 전 잔류부의 수용액 양 W₁은 279.55g, 증류 후 잔류부의 잔류액 양 W₂는 206.38g이다. Rayleigh식에 W₁, I₁, I₂를 이용해 W₂의 이론값을 계산해 보면 다음과 같다.

이어서 W₁, W₂(실험값, 이론값), x_auq, x_res 를 이용해 유출액의 평균 조성값을 실험값과 이론값으로 각각 계산해 보면 다음과 같다.

오차율에 대해 고찰해 보면 다음과 같은 주제로 정리될 수 있다.
1) 용액을 담은 비중병의 무게 측정 순서
이것은 실험 과정 중, 발생했을 수 있는 문제에 대한 생각이다. A1조는 이번 단증류 실험에서 증류 전, 순수 물과 순수 에탄올, 그리고 에탄올과 물이 잔류부에서 혼합된 수용액을 비중병에 담아 무게를 측정했다. 이 과정에서 A1조는 3가지 용액을 비커에 따라 비중병에 담을 준비를 한 뒤, 물, 에탄올, 수용액 순으로 무게를 측정했다. 이때 수용액을 담아둔 비커에 파라 필름 등을 씌워놓지 않았기 때문에 비중병에 물과 에탄올을 담아 무게를 측정하는 동안 수용액 속 휘발성이 강한 에탄올이 휘발되었을 수 있다. 따라서 빈 비커 + 수용액의 무게를 측정한 시점과 비중병에 수용액을 담아 무게를 측정한 시점의 수용액 속 에탄올의 조성이 다를 수 있을 가능성이 있다.
2) 수용액과 유출액의 온도 가정
A1조는 단증류 실험을 진행하는 과정에서 증류 전 잔류부에 담긴 수용액의 온도와 증류 후 충분히 식힌 유출액의 온도를 측정하지 않았다. 따라서 각 용액을 비중병에 담아 무게를 측정한 시점의 온도를 20℃로 가정해 실험 결과를 계산했기 때문에 실제 실험값과 계산에 사용된 실험값에 오차가 있을 수 있다. 실험 결과, 유출액의 평균 조성값의 실험값과 이론값의 오차율이 0%이기 위해 필요한 유출액과 수용액의 온도를 계산해 보면 다음과 같다.
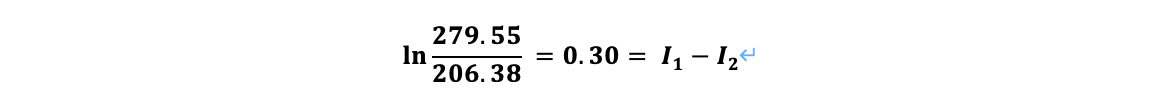
먼저 W₂의 이론값이 W₂의 실험값 206.38g이기 위해 위 식과 같이 (I₁ - I₂)의 값이 0.30이어야 한다. I₂값은 0.66이기 때문에 I₁값이 0.96이기 위해선 아래 그림5에서 파란 선으로 표시한 것과 같이 x_aqu 가 53%일 필요가 있다.
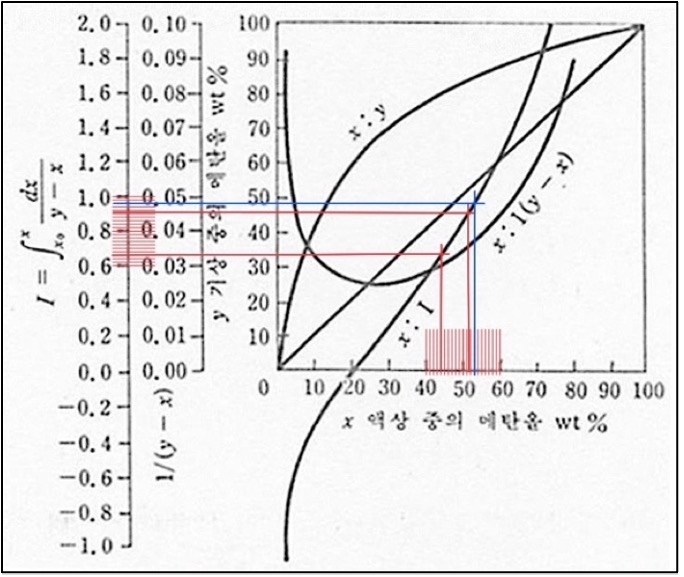
그림3, 온도에 따른 에탄올 밀도 표에서 밀도가 0.91이고, x_aqu가 53%인 경우, 수용액의 온도를 내삽을 통해 계산하면 다음과 같다.
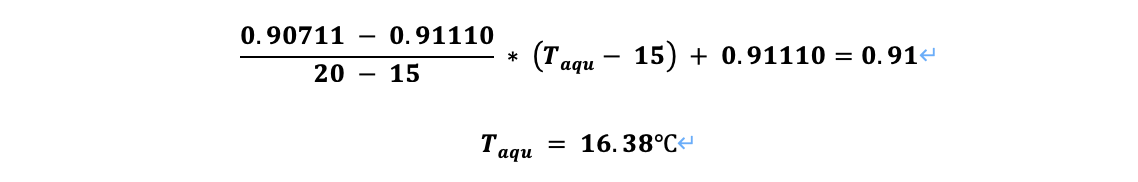
위같이 계산한 결과, 수용액의 온도는 16.38℃로 측정되었어야 오차율이 0%인 실험 결과를 도출할 수 있었다. 물론 위 계산 결과도 유출액의 온도를 20℃로 가정한 상태로 계산된 결과이기 때문에 정확하지 않다. 하지만 위같이 계산해 봄으로써 수용액과 유출액의 온도는 실험에서 가정한 20℃보다는 낮고, 16.38℃보다는 높이 측정되었어야 이번 A1조의 단증류 실험 결과의 오차율보다 낮은 오차율을 얻을 수 있음을 알 수 있었다.
3) 잔류액의 에탄올 조성 계산 결과
비중병에 잔류액을 담아 무게를 측정할 당시, 잔류액의 온도는 29℃였다. 온도에 따른 수용액 속 에탄올의 조성은 그림3과 같은 밀도 표로 계산했고, 그림3의 밀도 표에는 29℃일 때의 에탄올 조성은 표시되지 않았다. 따라서 그림3의 밀도 표를 통해 비중병 측정으로 계산된 밀도에 가장 가까운 두 온도의 밀도 값으로 수용액의 온도가 29℃인 경우에 해당하는 수용액 속 에탄올 조성을 계산했다. 이 과정에서 정확한 내삽이 이뤄지지 않았을 수 있다.
밀도 표에 표시된 온도는 각각 5℃의 간격을 두고 있다. 이때 같은 조성에서 온도에 따른 밀도값의 차이를 각 구간별로 비교해 보면 다음 표3과 같다.
| 에탄올 10wt%의 경우 | |
| 15℃ - 10℃ | 0.00089 |
| 20℃ - 15℃ | 0.00117 |
| 25℃ - 20℃ | 0.00144 |
| 30℃ - 25℃ | 0.00168 |
| 35℃ - 30℃ | 0.00190 |
표 3. 밀도표에서 각 온도 구간의 밀도 차이
표3을 보면 알 수 있듯이 온도에 따른 밀도 변화가 비선형적인 것을 알 수 있다. 따라서 단순 내삽을 통한 중간값 계산은 정확한 값을 나타내지 못함을 확인 가능하다. 그렇기 때문에 이번 단증류 실험 결과를 도출하는 과정에서 잔류액 속 에탄올 조성 계산 값이 실제 조성 값과 다를 수 있다는 것을 알 수 있다.
4) 손실액의 유무
증류 후, 잔류액과 유출액의 양을 확인했을 때, 손실이 9.58g으로 측정되었다. 이 손실의 대부분은 아래 그림6에서 확인 가능한 환류콕크 부분에 고인 유출액으로 예상된다. 증류되면서 유출부에 증류액이 차오르기 시작하면서 환류콕크 부분으로 증류액이 넘쳐들어가게 되면서 유출액의 양이 줄어드는 것이다.
만약 손실액이 유출액의 양으로 측정되었다면 오차율이 줄어들지 않았을까?, 측정된 잔류액의 양 W₂는 206.38g이었고, 측정된 손실액은 9.58g으로 이 둘의 합은 215.96g이다. 이는 이론값으로 계산된 W₂ 217.71g과 0.8%의 차이만을 보인다. 따라서 W₂의 실험값을 215.96g으로 가정하고 실험 결과를 계산하면 다음과 같다.

W₂가 계산 결과에서 영향을 끼치는 부분은 W₂의 실험값과 이론값의 오차율에 따른 유출액의 평균 조성값 오차율이다. 위와 같은 계산에 따르면 유출액의 평균 조성값 오차율은 1.23%로 기존의 오차율인 6.87%에 비해 5.64%p차이가 있음을 알 수 있다. 이는 기존의 오차율에 비해 82.1% 줄어든 결과인 것이다.
유출액의 양을 측정할 때, 유출부에 고인 손실액을 회수해 측정했다면 이것만으로도 이론값과 실험값의 오차율을 효과적으로 줄일 수 있었다는 것을 이번 계산을 통해 알게 되었다.
결론
| 양 [g] | 평균조성값 | |
| 실험 유출액 | 206.38 | 0.7360 |
| 이론 유출액 | 217.71 | 0.7903 |
| 오차율 | 5.49% | 6.87% |
표 4. 실험값과 이론값 간의 오차 결과
이번 실험에서는 잔류부에 에탄올 수용액을 담아 증류시켜 유출부에 냉각된 증류를 담아 유출부와 잔류부의 공간을 구분함으로써 증류 전, 후의 에탄올 조성 변화에 대해 알아보았다. 순수 물과 순수 에탄올의 밀도, 증류 전 잔류부의 수용액, 증류 후의 유출액과 잔류액의 밀도를 비중병을 통해 밀도를 측정함으로써 서로 비교한 결과, 에탄올의 조성이 (순수 에탄올 > 유출액 > 수용액 > 잔류액 > 순수 물)과 같은 순서로 많은 것을 알 수 있었다.
이 과정에서 측정된 수용액과 잔류액, 유출액의 양과 조성을 통해 실험값과 이론값의 오차를 확인할 수 있었고, 이론값은 Rayleigh식을 이용해 계산할 수 있었다. 계산 결과는 표4와 같이 양과 평균 조성값에 대해 각각 5.49%, 6.87%의 오차율이 계산되었다.
오차율에 대해 고찰해 본 결과, 수용액과 유출액의 온도를 가정함으로써 생기는 에탄올의 밀도 차이, 그리고 손실액의 회수 유무에 따라 오차율의 변화가 큰 것으로 판단했다. 먼저 수용액과 유출액의 온도를 20℃로 가정해 계산을 진행함으로 실제 온도와 차이가 발생해 계산 결과에 변화를 일으킨 것이다. 단순한 가정에 따른 계산이지만 수용액의 온도를 제외한 조건을 동일시 했을 때, 오차율이 0%이기 위해 필요한 수용액의 온도는 16.38℃인 것을 알 수 있었다. 가정했던 20℃에 비해 3.62℃ 차이가 난 결과고, 이는 수용액 또는 유출액의 온도가 16.38℃ 이상, 20℃ 미만일 때 더 적은 오차율을 얻을 수 있었음을 알 수 있다.
이어서 손실액 정도에 따른 오차율의 변화를 알아봤다. 유출액 양의 이론값은 206.38g이었고, 측정된 손실액은 9.58g으로 이 둘의 합은 215.96g이다. 이는 이론값으로 계산된 217.71g과 0.8%의 차이만을 보였고, 손실액의 대부분으로 예상되는 환류콕크 부분 고인 유출액을 회수함으로써 손실 없는 상황을 가정해 결과를 계산해 보면 오차율이 6.87%에서 1.23%로 상당히 줄어드는 것을 알 수 있었다.
참고문헌
1. 이영기, 한경대학교 화학공학과, 화학공학실험 단증류 실험, 2023.09.07
2. Warren L. McCabe 저, 허광선 외 5명 편역, 맥그로힐에듀케이션 코리아, “핵심단위조작”, 2018.01.29, 398~407p
3. McGraw-Hill 저, “American Institute of Physics Handbook”, 1957, 2-142p
'실험' 카테고리의 다른 글
| 열전도도 측정 실험 결과 보고서 (1) | 2024.12.08 |
|---|---|
| 레이놀즈 수 측정 실험 결과 보고서 (1) | 2024.12.07 |
| 기체 확산 계수 측정 실험 결과 보고서 (1) | 2024.11.26 |
| 프로판 탈 수소 반응 실험 결과 보고서 (0) | 2024.11.08 |
| 촉매특성분석 실험 결과 보고서 (0) | 2024.11.07 |




댓글