UV-vis의 원리
실험기기인 분광광도계는 사용하기에 매우 용이하고, 빠른 분석속도의 장점을 가지고 있다. 때문에 의약품 및 생명공학의 연구분야에서 가장 많이 사용되고 있는 분석용 기기 중 하나이며 이 분석기기는 많은 의약품 제약회사와 산업체에서 생산품이나 반응과정에 대한 화학적 정보를 얻는데 매우 유용하게 사용된다.
분광광도계를 이용한 분광광도법은 액상의 시료가 빛을 흡수하는 정도를 파장의 함수로 나타낸 측정방법으로 자외선, 가시광선 및 적외선 영역의 빛 등 특정파장의 빛과 물질의 상호작용을 기반으로 한 정량적 측정방법이다. 위와 같은 방법으로 측정한 측정값을 표현하기 위해 검량선을 이용하고, 검량선이란 표준액에 대해 나타나는 출력신호를 그래프로 표현한 것으로 정량분석에 사용된다. 농도를 알고 있는 각종의 표준액으로 분석 기기의 미터 지시도와 농도의 관계를 나타낸다.
흡광도
투광도란 광자의 흡수 입자 사이의 상호작용 결과이고, 그림1.과 같이 빛살의 세기는 P0에서 P로 감소한다. 평행복사선 빛살이 두께 b cm, 그리고 흡수화학종의 농도 c인 용액층을 통과하기 전후를 나타낸 것이다. 용액의 투광도 T는 용액을 투과한 입사복사선의 분율로 정의된다. 반대로 용액의 흡광도는 투광도와 통과 후의 빛살이 감소할수록 증가한다.

그림 1. 흡수용액에 의한 복사선 빛살의 감소
분광광도계를 이용해 흡광도를 분석하는 원리는 다음과 같다. 빛은 에너지의 한 형태이기 때문에 물질의 빛 흡수는 물질 내 분자 또는 원자의 에너지 수준을 높이게 되는데, 이때 일부 분자와 원자에서 광자가 다른 전자 에너지 수준 간 전이를 야기하게 된다. 흡수된 빛의 파장은 전자를 낮은 에너지 준위에서 높은 에너지 준위로 이동시킬 에너지를 갖고 있고, 이를 통해 파장을 알게 되면 빛을 흡수한 원자나 분자의 종류를 알 수 있다. 그림1.과 같이 용액에 빛을 통과 시킨 후 용액을 통과하기 전과 후의 빛의 세기를 비교해 흡광도를 분석하는데, 이때는 일반적으로 beer-lambert법칙을 이용한다.
beer-lambert법칙이란, 물질의 흡광도는 빛이 통과된 물질의 농도와 두께에 비례한다는 법칙이다. beer-lambert법칙에 의하면 단일 매질에 대한 흡광도를 다음과 같이 쓸 수 있다.

식 1. 흡광도 표현식
실험방법
1) 발색시약 제조
1. 메타바나드산 암모늄 0.56g + 증류수 100ml + 질산 125ml
2. 몰리브덴산 암모늄 13.5g + 증류수 100ml
3. 500ml 부피 플라스크에 1, 2번 용액 주입 후, 표선까지 증류수로 채우고, 파라필름 씌운 후 대기
2) 표준용액 제조
1. 제일인산칼륨 1.9369g + 약간의 증류수 넣어 용해 후 1L 부피 플라스크에 용액을 넣고 표선까지 증류수로 채움 (1000ppm 용액)
2. 1번 용액을 25ml 취해 250ml 부피 플라스크에 넣고 표선까지 증류수로 채워 100ppm 농도로 희석
3. 100ml 부피 플라스크에 blank(0ppm), 표준용액(5ppm, 10ppm, 15ppm)을 제조 후, 발색시약(20ml)를 넣고 표선까지 증류수 채운 후, 대기
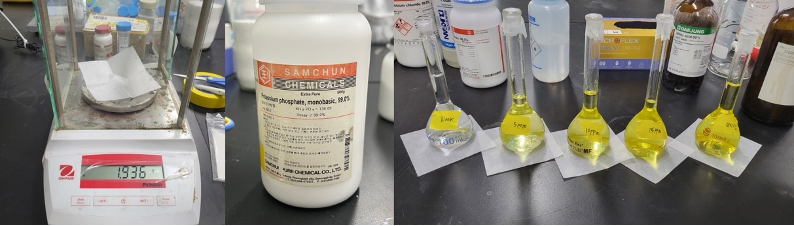
그림 2. 표준용액 제조 과정
3) 미지 시료 제조 및 미지 시료 용액 희석
1. 제일인산암모늄 0.412g + 증류수 100ml
2. 염산 30ml + 질산 10ml + 약간의 증류수 넣어 모두 용해
3. 1L 부피 플라스크에 넣고 표선까지 증류수를 채운 후, 파라필름으로 막고 대기
4. 100ml 부피 플라스크에 희석한 미지 시료 용액(5ml)과 발색 시약(20ml) 넣고 표선까지 증류수 채운 후, 대기 (이때, 미지시료를 5ml 넣는 이유는 미지시료의 농도를 표준용액의 농도범위인 0~15ppm 사이와 같이 만들기 위해서다.)

그림 3. 미지시료용액 제조 과정
4) 흡광도 측정
1. 큐벳(cell) 한 개를 준비하고 각각 피펫을 이용해 큐벳 용량의 3/4만큼 채워 넣는다. 이때, 큐벳에 빗살무늬가 있는 곳은 빛이 통과하지 않는 부분이므로 이 부위를 잡는다. (빛의 통과면은 지문이나 이물질이 묻지 않도록 하며, 측정 후 다음 측정할 용액으로 큐벳을 행궈준 후 측정을 진행한다.)
2. 분광광도계를 이용해 흡광도를 측정한다.
실험결과

그림 4. ppm에 따른 각 표준용액의 흡광도 그래프
| No. | Conc[ppm] | Abs | 415.0nm |
| Blank | 0.0743 | ||
| 1 | 5 | 0.141985 | 0.1420 |
| 2 | 10 | 0.259795 | 0.2598 |
| 3 | 15 | 0.383196 | 0.3832 |
표 1. 각 ppm별 흡광도 측정 결과
| No. | Mode | Conc[ppm] | Abs | 415.0nm |
| 1 | Blank-1 | 0.0743 | ||
| 2 | Sample-1 | 14.4041 | 0.372689 | 0.3727 |
| 3 | Sample-2 | 14.3966 | 0.372494 | 0.3725 |
표 2. 미지시료 흡광도 측정 결과
그림4의 그래프를 보면 ppm이 높을수록, 즉, 용액의 농도가 진할수록 흡광도 또한 높아지는 것을 확인할 수 있다. 표2와 같이 미지시료 용액의 흡광도 측정 결과, 이전 실험에 비해 농도가 진한 것을 확인했고, 이에 잘못된 결과는 아닌지 확인하기 위해 미지시료 용액의 흡광도를 2회 측정하였다. 결과, 2회 모두 거의 같은 값이 나와 올바른 결과임을 확인했고, 따라서 미지시료의 농도 측정값은 14.4ppm으로 확인되었다.
농도가 1000ppm인 표준용액 제조시, 필요한 제일인산칼륨(KH2PO4)의 양이 1.9369g인 이유는 다음과 같다. 제일인산칼륨을 용해시키면 식2와 같이 제일인산칼륨 2몰 당, 인산(P2O5)이 1몰 생성되기 때문에 이에 따라 용액 1L에 필요한 인산 1g을 얻기 위해 필요한 제일인산칼륨은 식3과 같이 1.9369g이 필요하게 된다.
2KH2PO4 -> P2O5 + 2H2O + K2O
식 2. 제일인산칼륨 용해시 반응식

식 3. 1g의 인산을 얻기 위해 필요한 제일인산칼륨 질량 계산
이번 실험에 쓰인 제일인산칼륨은 그림2와 같이 순도99%를 쓰기 때문에 위와 같이 계산하면 x = 1.9369g으로 필요한 제일인산칼륨의 양과 같다.
이에 따라 미지시료의 농도를 구해보면 다음과 같다. 미지시료로 쓰인 제일인산암모늄 또한 용해시 2몰 당, 인산을 1몰 생성하고, 그림3과 같이 순도가 98%인 제일인산암모늄 0.412g을 첨가했다. 식4에 따라 x = 0.2491g이므로 미지시료 용액 속 포함된 인산의 양과 같다. 따라서 실험과정 3-3까지의 미지시료 용액 농도는 249.1ppm이고, 실험과정 3-4와 같이 농도를 희석해주면 식5와 같다.

식 4. 1g의 인산을 얻기 위해 필요한 제일인산암모늄 질량 계산

식 5. 희석 후 용액 속 인산 농도 계산
희석 후, 이론적인 용액 속 인산 농도는 12.455ppm인 것을 알 수 있으므로, 실제로 측정한 미지시료 용액의 농도와의 오차율은 얼마인지 계산해보면 식6과 같이 15.616%인 것을 확인할 수 있다.
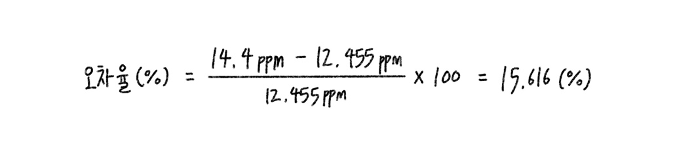
식 6. 실제로 측정된 농도값과 이론상 농도값의 오차율 계산
이어서 표3과 표4를 참고해 회귀방정식을 세우고, 검정곡선을 그리며, 상관계수를 구할 수 있다. 표3은 각 시료별 측정한 흡광도를 보정한 것이고, 표4는 보정한 흡광도를 포함하여 계산에 필요한 값들을 정리한 표이다.
| Blank | 5ppm | 10ppm | 15ppm | 미지시료 | |
| 각 흡광도 | 0.0743 | 0.141985 | 0.259795 | 0.383196 | 0.372689 |
| Blank흡광도 | 0.0743 | 0.0743 | 0.0743 | 0.0743 | 0.0743 |
| 보정 흡광도 | 0 | 0.067685 | 0.185495 | 0.308896 | 0.298389 |
표 3. 흡광도 결과표
| X | Y | X^2 | Y^2 | XY | |
| STD1 | 5 | 0.067685 | 25 | 0.004581 | 0.338425 |
| STD2 | 10 | 0.185495 | 100 | 0.034408 | 1.854950 |
| STD3 | 15 | 0.308896 | 225 | 0.095417 | 4.633440 |
| 총 합 | 30 | 0.562076 | 350 | 0.134406 | 6.826815 |
표 4. 분석을 위한 결과표 정리
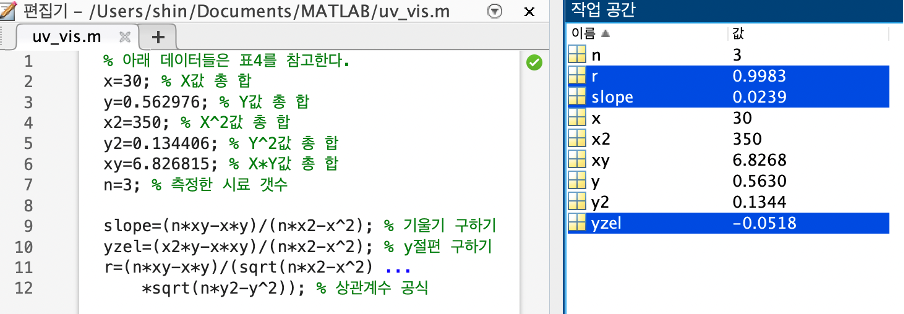
그림 5. 매트랩을 이용해 계산한 결과
계산이 복잡하기 때문에 그림5와 같이 매트랩을 이용해 계산을 진행했다. 계산 결과, 기울기(slope)는 0.0239, y절편(yzel)은 -0.0518, 상관계수(r)는 0.9983이 나왔다. 측정값으로 나온 상관계수인 0.99991과 실제 상관계수 계산값 0.9983과의 오차율은 0.17%미만인 것을 확인할 수 있다. 따라서 회귀방정식은 아래 식7과 같다.
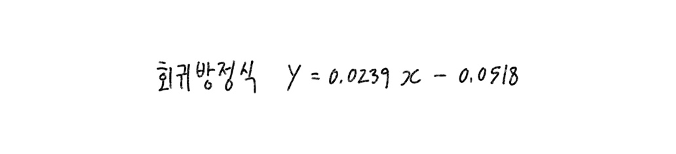
식 7. 회귀방정식 결과
식7의 회귀방정식 Y에 미지시료 용액의 보정 흡광도값인 0.298389를 넣어 계산하면 X는 14.6251ppm인 것을 알 수 있고, 이 것을 회귀방정식과 함께 그래프로 표현하면 그림6과 같다. 그림6 그래프 속 미지시료 용액의 보정흡광도에 따른 농도의 데이터 팁을 보면 계산한 것과 같이 보정 흡광도 0.298389에 따른 ppm값이 14.6251인 것을 확인 할 수 있다. 따라서 보정된 값을 통해 다시 한번 이론적 미지시료 속 인산 농도와의 오차율을 구해보면 아래 식8과 같다.
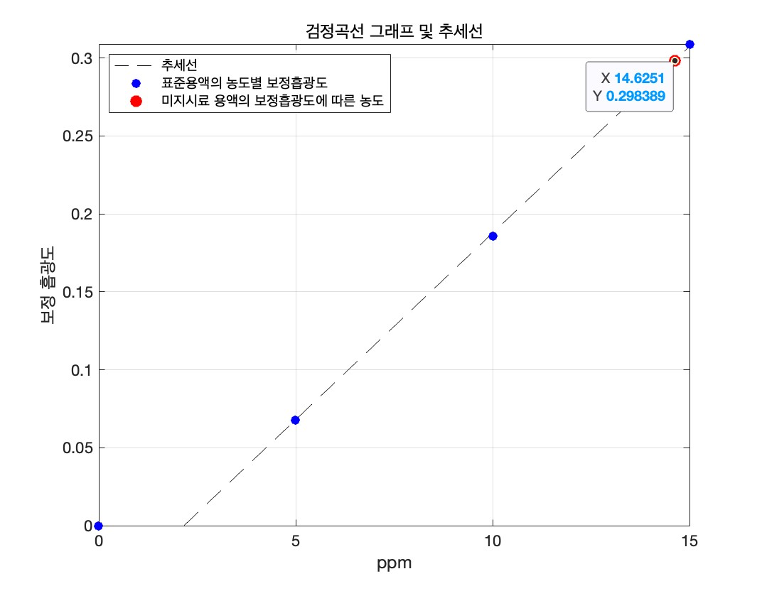
그림 6. 검정곡선 그래프 및 추세선
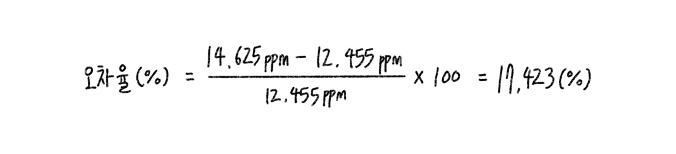
식 8. 보정된 농도값과 이론상 농도값의 오차율 계산
식8을 통해 보정된 농도값과 이론상 농도값의 오차율은 17.423%로 보정 전 농도값과의 오차율에 비해 오차율이 1.807%p 높아진 것을 확인 할 수 있다.
추가로 인산 함량을 계산해보면 다음과 같다. 이론적으로 인산의 함량은 식9와 같이 61.7%이다. 따라서 식7을 통해 알게 된 보정된 농도값을 이용해 미지시료 용액의 인산 농도를 희석배수를 고려하여 계산하면 식10과 같이 미지시료 속 인산 함량은 70.1%인 것을 확인 할 수 있다.
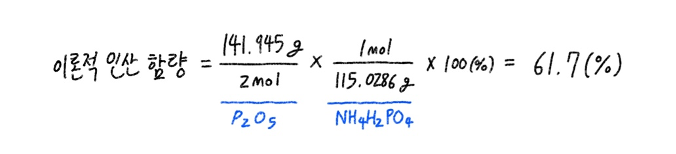
식 9. 이론적 인산 함량 계산식

식 10. 실제 미지시료 속 인산 함량 계산식
따라서 이번 실험에서 미지시료 속 인산 함량의 실제값은 이론값과 8.4%p차이가 나고, 인산 함량 오차율은 다음 식11과 같이 13.614%인 것을 확인 할 수 있다.
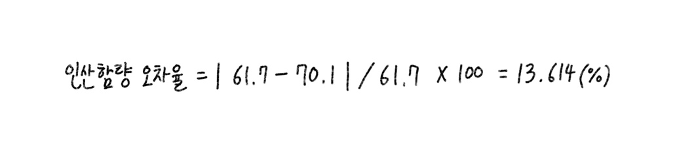
식 11. 인산 함량 오차율
고찰 및 결론
이번 실험 결과로써 확인 할 수 있는 미지시료 속 인산 농도 및 상관계수 등의 데이터를 살펴보면, 표준용액 제조에서의 문제는 없었지만 미지시료를 제조하는 과정에서 오차가 났음을 알 수 있다. 그림4와 그림5를 보면 알 수 있듯, 상관계수는 1에 근접하고, 측정값과 계산값의 오차율 또한 0.17% 미만으로, 추세선과 표준용액의 농도별 흡광도의 관계가 선형에 가까운 결과임을 확인 할 수 있다. 하지만 미지시료 속 인산 농도는 식5에서부터 실제 측정값과는 확연히 다른 값을 확인해 볼 수 있었다. 따라서 측정값과 계산값 간의 오차율 또한 15%가 넘는 오차를 보였고, 식8을 통해 알 수 있듯, 흡광도를 보정 후 계산한 값을 통해서도 더 높은 오차율인 17.423%를 확인 할 수 있었다. 결과적으로 이번 실험의 미지시료 속 인산 함량은 이론적 값과는 13.614%의 오차율인 70.1%을 갖게 되었다.
그렇다면 미지시료 속 인산 함량에 대한 오차는 왜 발생했는가에 대한 생각을 해볼 수 있다. 먼저 실험과정 중, 3-2에서 3-3으로 넘어가는 과정에서 지체된 시간이 약 30분을 넘겼다. 실험과정 3-2에서 제조하는 용액은 진한 염산과 진한 질산을 3:1로 섞어 만든 왕수인데, 이 것은 제조 직후 바로 사용하지 않으면 용액 내 반응으로 인해 염화 니트로실 성분이 분해됨으로써 왕수의 특성을 잃는다. 그리고 이때 사용된 염산의 농도는 35~37%로 끓는점이 약 61℃이고, 질산의 농도는 60%로 끓는점이 약 83℃이다. 이는 실험 과정이 넘어가기 전 지체된 30분을 통해 증발되거나, 왕수로써 특성을 잃기 충분한 시간이라고 생각한다. 실험 당시에는 이를 인지하지 못하고 지체된 시간 후의 왕수를 그대로 미지시료를 제조하는데 써버렸고, 이 과정이 실험 결과에 영향을 미쳤을 것이라고 생각한다.
또한 미지시료를 1L 부피 플라스크에 제조할 때, 용액들을 조금씩 넣어가며 섞은 후에 증류수를 채운 것이 아닌, 한번에 용액들을 넣고, 부피 플라스크의 표선까지 증류수를 넣은 후, 용액을 섞은 결과, 미지시료의 함량이 균일하지 못한 상태로 실험을 진행했을 확률이 충분하다고 생각하기 때문에 이것 또한 실험 결과에 영향을 미쳤을 것이라고 생각한다.
이번 실험을 통해 인산전량 정량 분석 실험 과정에 대해 배울 수 있었고, 흡광광도법에 의한 흡광도 측정으로 농도와 흡광도 간 관계를 직접 체감할 수 있었다. 농도가 진할수록 흡광도 값 또한 높아지며, 이는 결과가 선형적인 관계를 띄었을 때, 흡광도로부터 정확한 농도를 구할 수 있음을 알 수 있었다. 이를 통해 혹시나 실험의 중간 결과로써 농도를 측정할 시, 이론값을 계산해 실제 실험값과 이론값 사이에 괴리가 있다면 이를 선제적으로 인지함으로써 실험 결과의 방향을 조정할 수 있을 것 같다는 생각을 했다.
또한 실험을 진행함으로써 농도와 흡광도 간의 관계를 더 알아본 결과, 일반적으로는 용액의 농도가 높을수록 흡광도 또한 높아지지만, 일정 농도 이상부터는 용액 내 분자들의 이론적인 흡광도 상한선을 초과하여 측정값이 실제 흡광도와 다르게 나타날 수 있다. 이는 흡광도와 농도의 관계가 비선형적인 관계가 되는 것을 의미하고, 따라서 이런 상태일때는 흡광도를 통해 농도를 정확하게 구하는 것은 타당하지 못하다는 의미가 된다. 때문에 실험에서 표준용액과 미지시료 용액을 왜 희석하며 실험을 진행하는지에 대해 알 수 있었다.
참고문헌
(1) 김경옥, 강영구 외 1명 저, “UV-VIS 분광기기의 성능검증을 위한 밸리데이션 가이드라인의 제정 및 응용”, 조선대학교, 약학대학, 154p, 2006.
(2) 여아름 저, “분광광도법에 의한 착색 염료 및 렌즈 연구”, 건양대학교, 보건복지대학원, 3p~5p, 2010.
(3) 황수연 저, lecture 10 분광광도법, 한경대학교, 화학공학과, 2021.05.09.
(4) 황수연 저, lecture 10-1 분석기사 작업형, 한경대학교, 화학공학과, 2021.05.09.
(5) NAVER 지식백과, 검량선, https://terms.naver.com/entry.naver?docId=3391264&cid=60289&categoryId=60289
(6) WIKIPEDIA, 비어-람베르트 법칙, https://ko.wikipedia.org/wiki/%EB%B9%84%EC%96%B4-%EB%9E%8C%EB%B2%A0%EB%A5%B4%ED%8A%B8_%EB%B2%95%EC%B9%99
(7) WIKIPEDIA, 왕수, https://ko.wikipedia.org/wiki/%EC%99%95%EC%88%98
'실험' 카테고리의 다른 글
| 기체 확산 계수 측정 실험 결과 보고서 (1) | 2024.11.26 |
|---|---|
| 프로판 탈 수소 반응 실험 결과 보고서 (0) | 2024.11.08 |
| 촉매특성분석 실험 결과 보고서 (0) | 2024.11.07 |
| PS 중합 실험, 화학반응실험 결과 보고서 (0) | 2024.02.17 |
| 일산화탄소 산화 반응 실험 결과 보고서 (0) | 2023.05.14 |




댓글